Quantum Versus Classical Proofs and Advice
by Scott Aaronson and Greg Kuperberg
Theory of Computing, Volume 3(7), pp. 129-157, 2007
Bibliography with links to cited articles
[1] S. Aaronson: Quantum copy-protection. In preparation.
[2] S. Aaronson: Limitations of quantum advice and one-way communication. Theory of Computing, 1:1–28, 2005. quant-ph/0402095. Conference version in Proc. of CCC’2004. [ToC:v001/a001, arXiv:quant-ph/0402095].
[3] D. Aharonov and T. Naveh: Quantum NP - a survey. quant-ph/0210077, 2002. [arXiv:quant-ph/0210077].
[4] L. Babai: Trading group theory for randomness. In Proc. 17th STOC, pp. 421–429, 1985. [STOC:10.1145/22145.22192].
[5] L. Babai: Bounded round interactive proofs in finite groups. SIAM J. Discrete Math, 5(1):88–111, 1992. [SIDMA:10.1137/0405008].
[6] L. Babai and P. Erd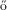 s: Representation of group elements as short
products. Annals of Discrete Math., 12:27–30, 1982.
s: Representation of group elements as short
products. Annals of Discrete Math., 12:27–30, 1982.
[7] L. Babai, A. J. Goodman, W. M. Kantor, E. M. Luks, and P. P. Pálfy: Short presentations for finite groups. J. Algebra, 194:79–112, 1997. [Elsevier:10.1006/jabr.1996.6980].
[8] L. Babai and E. Szemerédi: On the complexity of matrix group problems I. In Proc. 25th FOCS, pp. 229–240, 1984.
[9] M. Ben-Or, D. Coppersmith, M. Luby, and R. Rubinfeld: Non-abelian homomorphism testing, and distributions close to their self-convolutions. In Proc. of 8th Intern. Workshop on Randomization and Computation (RANDOM’04), pp. 273–285. Springer-Verlag, 2004. ECCC TR04-052. [Springer:x1tlgm3cexcj].
[10] C. Bennett, E. Bernstein, G. Brassard, and U. Vazirani: Strengths and weaknesses of quantum computing. SIAM J. Computing, 26(5):1510–1523, 1997. quant-ph/9701001. [SICOMP:10.1137/S0097539796300933, arXiv:quant-ph/9701001].
[11] K. Böröczky Jr. and G. Wintsche: Covering the sphere by equal spherical balls. In Discrete and Computational Geometry: The Goodman-Pollack Festschrift, pp. 237–253. Springer, 2003.
[12] G. Brassard, P. Høyer, M. Mosca, and A. Tapp: Quantum amplitude amplification and estimation. In S. J. Lomonaco and H. E. Brandt, editors, Quantum Computation and Information, Contemporary Mathematics Series. AMS, 2002. quant-ph/0005055. [arXiv:quant-ph/0005055].
[13] J. H. Conway, R. T. Curtis, S. P. Norton, R. A. Parker, and R. A. Wilson: Atlas of Finite Groups. Clarendon Press, Oxford, 1985.
[14] M. Ettinger, P. Høyer, and E. Knill: The quantum query complexity of the hidden subgroup problem is polynomial. Inform. Proc. Lett., 91(1):43–48, 2004. quant-ph/0401083. [IPL:10.1016/j.ipl.2004.01.024, arXiv:quant-ph/0401083].
[15] L. K. Grover: A framework for fast quantum mechanical algorithms. In Proc. 30th STOC, pp. 53–62, 1998. quant-ph/9711043. [STOC:10.1145/276698.276712, arXiv:quant-ph/9711043].
[16] S. Hallgren, A. Russell, and A. Ta-Shma: The hidden subgroup problem and quantum computation using group representations. SIAM J. Computing, 32(4):916–934, 2003. Conference version in STOC’2000, p. 627-635. [SICOMP:10.1137/S009753970139450X].
[17] B. Höfling: Efficient multiplication algorithms for finite polycyclic groups, 2007. Submitted. www-public.tu-bs.de/~bhoeflin/preprints/collect.pdf.
[18] A. Hulpke and Á. Seress: Short presentations for three-dimensional unitary groups. J. Algebra, 245:719–729, 2001. [Elsevier:10.1006/jabr.2001.8943].
[19] J. Kempe, A. Kitaev, and O. Regev: The complexity of the Local Hamiltonian problem. SIAM J. Computing, 35(5):1070–1097, 2006. quant-ph/0406180. [SICOMP:10.1137/S0097539704445226, arXiv:quant-ph/0406180].
[20] A. Kitaev: Quantum measurements and the abelian stabilizer problem. ECCC TR96-003, quant-ph/9511026, 1996. [arXiv:quant-ph/9511026].
[21] A. Kitaev: Quantum computation: algorithms and error correction. Russian Math. Surveys, 52(6):1191–1249, 1997.
[22] C. Marriott and J. Watrous: Quantum Arthur-Merlin games. Computational Complexity, 14(2):122–152, 2005. [CC:h0521k6666871652].
[23] C. Moore, D. N. Rockmore, and A. Russell: Generic quantum Fourier transforms. In Proc. 15th Ann. ACM-SIAM Symp. on Discrete Algorithms, pp. 778–787, 2004. quant-ph/0304064. [SODA:982792.982910, arXiv:quant-ph/0304064].
[24] M. Mosca and D. Stebila: Unforgeable quantum money. In preparation, 2006.
[25] P. M. Neumann: An enumeration theorem for finite groups. Quart. J. Math. Ser., 2(20):395–401, 1969.
[26] L. Pyber: Enumerating finite groups of given order. Annals of Mathematics, 137:203–220, 1993.
[27] R. Raz and A. Shpilka: On the power of quantum proofs. In Proc. 19th Ann. IEEE Conf. on Computational Complexity, pp. 260–274, 2004. [CCC:10.1109/CCC.2004.1313849].
[28] A. Shamir: IP=PSPACE. J. ACM, 39(4):869–877, 1992. [JACM:10.1145/146585.146609].
[29] P. Shor: Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM J. Computing, 26(5):1484–1509, 1997. Earlier version in IEEE FOCS 1994. quant-ph/9508027. [SICOMP:10.1137/S0097539795293172, arXiv:quant-ph/9508027].
[30] C. Sims: Computational methods in the study of permutation groups. In Computational Problems in Abstract Algebra, pp. 169–183. Pergamon Press, 1970.
[31] J. Watrous: Succinct quantum proofs for properties of finite groups. In Proc. 41st FOCS, pp. 537–546, 2000. cs.CC/0009002. [FOCS:10.1109/SFCS.2000.892141].
