Limitations of Quantum Advice and One-Way Communication
Theory of Computing, Volume 1(1), pp. 1-28, 2005
Bibliography with links to cited articles
[1] S. Aaronson: Quantum lower bound for the collision problem. In Proc. 34th ACM STOC, pp. 635–642, 2002. [STOC:509907.509999, arXiv:quant-ph/0111102].
[2] S. Aaronson: Limitations of quantum advice and one-way communication. In 19th IEEE Conf. Comput. Complexity (CCC), pp. 320–332, 2004. [CCC:10.1109/CCC.2004.1313854, arXiv:quant-ph/0402095].
[3] S. Aaronson: Quantum computing, postselection, and probabilistic polynomial-time. Submitted, 2004. [arXiv:quant-ph/0412187].
[4] L. Adleman, J. DeMarrais, and M.-D. Huang: Quantum computability. SIAM J. Computing, 26(5):1524–1540, 1997. [SICOMP:10.1137/S0097539795293639].
[5] A. Ambainis, A. Nayak, A. Ta-Shma, and U. V. Vazirani: Quantum dense coding and quantum finite automata. J. ACM, 49:496–511, 2002. Earlier version in 31st ACM STOC, 1999, pp. 376-383. [JACM:581771.581773, arXiv:quant-ph/9804043].
[6] Z. Bar-Yossef, T. S. Jayram, and I. Kerenidis: Exponential separation of quantum and classical one-way communication complexity. In 36th ACM STOC, pp. 128–137, 2004. [STOC:1007352.1007379, ECCC:TR04-036].
[7] R. Beals, H. Buhrman, R. Cleve, M. Mosca, and R. de Wolf: Quantum lower bounds by polynomials. J. ACM, 48(4):778–797, 2001. Earlier version in 39th IEEE FOCS, 1998, pp. 352-361. [JACM:502090.502097, arXiv:quant-ph/9802049].
[8] C. Bennett, E. Bernstein, G. Brassard, and U. Vazirani: Strengths and weaknesses of quantum computing. SIAM J. Computing, 26(5):1510–1523, 1997. [SICOMP:30093, arXiv:quant-ph/9701001].
[9] C. H. Bennett, G. Brassard, C. Crépeau, R. Jozsa, A. Peres, and W. Wootters: Teleporting an unknown quantum state by dual classical and EPR channels. Phys. Rev. Lett., 70:1895–1898, 1993. [PRL:10.1103/PhysRevLett.70.1895].
[10] C. H. Bennett and J. Gill: Relative to a random oracle A,
PA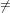 NPA
NPA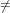 coNPA with probability 1. SIAM J. Computing,
10(1):96–113, 1981. [SICOMP:10/0210008].
coNPA with probability 1. SIAM J. Computing,
10(1):96–113, 1981. [SICOMP:10/0210008].
[11] S. N. Bernstein: Sur l’ordre de la meilleure approximation des fonctions continues par les polynômes de degré donné. Mem. Cl. Sci. Acad. Roy. Belg., 4:1–103, 1912. French.
[12] H. Buhrman, R. Cleve, J. Watrous, and R. de Wolf: Quantum fingerprinting. Phys. Rev. Lett., 87(16), 2001. 4 pages. [PRL:10.1103/PhysRevLett.87.167902, arXiv:quant-ph/0102001].
[13] H. Buhrman and R. de Wolf: Complexity measures and decision tree complexity: a survey. Theoretical Computer Sci., 288:21–43, 2002. [TCS:10.1016/S0304-3975(01)00144-X].
[14] P. Duriš, J. Hromkovič, J. D. P. Rolim, and G. Schnitger: Las Vegas versus determinism for one-way communication complexity, finite automata, and polynomial-time computations. In 14th Symp. Theoret. Aspects of Comp.Sci. (STACS), pp. 117–128, 1997.
[15] H. Ehlich and K. Zeller: Schwankung von Polynomen zwischen Gitterpunkten. Mathematische Zeitschrift, 86:41–44, 1964.
[16] L. Fortnow and J. Rogers: Complexity limitations on quantum computation. J. Comput. Sys. Sci., 59(2):240–252, 1999. [JCSS:10.1006/jcss.1999.1651, arXiv:cs.CC/9811023].
[17] O. Goldreich: On quantum computing. 2004. 1 page.
[18] Y. Han, L. Hemaspaandra, and T. Thierauf: Threshold computation and cryptographic security. SIAM J. Computing, 26(1):59–78, 1997. [SICOMP:24046].
[19] A. S. Holevo: Some estimates of the information transmitted by quantum communication channels. Problems of Information Transmission, 9:177–183, 1973. English translation.
[20] H. Klauck: Quantum communication complexity. In 27th Int’l. Colloq. on Automata, Languages, and Programming (ICALP), pp. 241–252, 2000. [arXiv:quant-ph/0005032].
[21] H. Klauck: Quantum time-space tradeoffs for sorting. In 35th ACM STOC, pp. 69–76, 2003. [STOC:780542.780553, arXiv:quant-ph/0211174].
[22] H. Klauck, R. Špalek, and R. de Wolf: Quantum and classical strong direct product theorems and optimal time-space tradeoffs. In 45th IEEE FOCS, pp. 12–21, 2004. [FOCS:10.1109/FOCS.2004.52, arXiv:quant-ph/0402123].
[23] E. Kushilevitz and N. Nisan: Communication Complexity. Cambridge, 1997.
[24] A. A. Markov: On a question by D. I. Mendeleev. Zapiski Imperatorskoi Akademii Nauk, SP6(62):1–24, 1890. Russian. English translation at http://www.math.technion.ac.il/hat/fpapers/markov4.pdf.
[25] V. A. Markov: Über Polynome, die in einem gegebenen Intervalle möglichst wenig von Null abweichen. Math. Ann., 77:213–258, 1916. German. Originally written in 1892.
[26] M. Minsky and S. Papert: Perceptrons (2nd edition). MIT Press, 1988. First appeared in 1968.
[27] A. Nayak: Optimal lower bounds for quantum automata and random access codes. In 40th IEEE FOCS, pp. 369–377, 1999. [FOCS:10.1109/SFFCS.1999.814608, arXiv:quant-ph/9904093].
[28] M. Nielsen and I. Chuang: Quantum Computation and Quantum Information. Cambridge University Press, 2000.
[29] N. Nisan and M. Szegedy: On the degree of Boolean functions as real polynomials. Computational Complexity, 4(4):301–313, 1994.
[30] H. Nishimura and T. Yamakami: Polynomial time quantum computation with advice. Inform. Proc. Lett., 90:195–204, 2003. [IPL:10.1016/j.ipl.2004.02.005, ECCC:TR03-059, arXiv:quant-ph/0305100].
[31] M. Rabin and A. C-C. Yao: Manuscript, cited in [38], 1979.
[32] T. J. Rivlin: Chebyshev Polynomials: From Approximation Theory to Algebra and Number Theory. Wiley, 1990.
[33] T. J. Rivlin and E. W. Cheney: A comparison of uniform approximations on an interval and a finite subset thereof. SIAM J. Numerical Analysis, 3(2):311–320, 1966. [SINUM:03/0703024].
[34] N. Sauer: On the density of families of sets. J. Combinatorial Theory Series A, 13:145–147, 1972. [JCombThA:10.1016/0097-3165(72)90019-2].
[35] Y. Shi: Both Toffoli and controlled-NOT need little help to do universal quantum computation. Quantum Information and Computation, 3(1):84–92, 2002. [arXiv:quant-ph/0205115].
[36] J. Watrous: Succinct quantum proofs for properties of finite groups. In 41st IEEE FOCS, pp. 537–546, 2000. [FOCS:10.1109/SFCS.2000.892141, arXiv:cs.CC/0009002].
[37] A. Winter: Quantum and classical message identification via quantum channels. In O. Hirota, editor, Quantum Information, Statistics, Probability (A. S. Holevo festschrift), pp. 172–189. Rinton, 2004. [arXiv:quant-ph/0401060].
[38] A. C-C. Yao: Some complexity questions related to distributive computing. In 11th ACM STOC, pp. 209–213, 1979. [STOC:804414].
[39] A. C-C. Yao: Princeton University course assignment, 2001.
[40] A. C-C. Yao: On the power of quantum fingerprinting. In 35th ACM STOC, pp. 77–81, 2003. [STOC:780542.780554, ECCC:TR02-074].
