[1]   Eric Allender, David A. Mix Barrington, Tanmoy Chakraborty, Samir Datta, and Sambuddha Roy: Planar and grid graph reachability problems. Theory Computing Sys., 45(4):675–723, 2009. [doi:10.1007/s00224-009-9172-z]

[2]   Eric Allender and Meena Mahajan: The complexity of planarity testing. Inform. Comput., 189(1):117–134, 2004. Preliminary version in STACS’00. [doi:10.1016/j.ic.2003.09.002]

[3]   Tetsuo Asano and Benjamin Doerr: Memory-constrained algorithms for shortest path problem. In Proc. 23rd Canad. Conf. Comput. Geom. (CCCG’11), pp. 1–4, 2011. cccg.ca.

[4]   Tetsuo Asano, David Kirkpatrick, Kotaro Nakagawa, and Osamu Watanabe: Õ(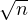)-space and polynomial-time algorithm for planar directed graph reachability. In Proc. Internat. Symp. Math. Foundations of Comp. Sci. (MFCS’14), pp. 45–56. Springer, 2014. [doi:10.1007/978-3-662-44465-8_5, ECCC:TR14-071]

[5]   Ryo Ashida and Kotaro Nakagawa: Õ(n^1∕3)-space algorithm for the grid graph reachability problem. In Proc. 34th Internat. Symp. Comput. Geom. (SoCG’18), pp. 5:1–13. Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik, 2018. [doi:10.4230/LIPIcs.SoCG.2018.5, arXiv:1803.07097]

[6]   Greg Barnes, Jonathan F. Buss, Walter L. Ruzzo, and Baruch Schieber: A sublinear space, polynomial time algorithm for directed s-t connectivity. SIAM J. Comput., 27(5):1273–1282, 1998. Preliminary version in SCT’92. [doi:10.1137/S0097539793283151]

[7]   Diptarka Chakraborty, Aduri Pavan, Raghunath Tewari, N. V. Vinodchandran, and Lin F. Yang: New time-space upperbounds for directed reachability in high-genus and H-minor-free graphs. In Proc. 34th Found. Softw. Techn. Theoret. Comp. Sci. Conf. (FSTTCS’14), pp. 585–595. Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik, 2014. [doi:10.4230/LIPIcs.FSTTCS.2014.585, ECCC:TR14-035]

[8]   Diptarka Chakraborty and Raghunath Tewari: An O(n^ϵ) space and polynomial time algorithm for reachability in directed layered planar graphs. ACM Trans. Comput. Theory, 9(4):19:1–11, 2017. Preliminary version in ISAAC’15. [doi:10.1145/3154857, arXiv:1501.05828, ECCC:TR15-016]

[9]   Tatsuya Imai, Kotaro Nakagawa, Aduri Pavan, N. V. Vinodchandran, and Osamu Watanabe: An O(n^+ϵ)-space and polynomial-time algorithm for directed planar reachability. In Proc. 28th IEEE Conf. on Comput. Complexity (CCC’13), pp. 277–286. IEEE Comp. Soc., 2013. [doi:10.1109/CCC.2013.35]

[10]   Rahul Jain and Raghunath Tewari: An O(n^1∕4+ϵ) space and polynomial algorithm for grid graph reachability. In Proc. 39th Found. Softw. Techn. Theoret. Comp. Sci. Conf. (FSTTCS’19), pp. 19:1–14. Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik, 2019. [doi:10.4230/LIPIcs.FSTTCS.2019.19]

[11]    Sampath Kannan, Sanjeev Khanna, and Sudeepa Roy: STCON in directed unique-path graphs. In Proc. 28th Found. Softw. Techn. Theoret. Comp. Sci. Conf. (FSTTCS’08), pp. 256–267. Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik, 2008. [doi:10.4230/LIPIcs.FSTTCS.2008.1758]

[12]   Gary L. Miller: Finding small simple cycle separators for 2-connected planar graphs. J. Comput. System Sci., 32(3):265–279, 1986. Preliminary version in STOC’84. [doi:10.1016/0022-0000(86)90030-9]

[13]   Omer Reingold: Undirected connectivity in log-space. J. ACM, 55(4):17:1–24, 2008. Preliminary version in STOC’05. [doi:10.1145/1391289.1391291]

[14]   Walter J. Savitch: Relationships between nondeterministic and deterministic tape complexities. J. Comput. System Sci., 4(2):177–192, 1970. [doi:10.1016/S0022-0000(70)80006-X]

[15]   Derrick Stolee and N. V. Vinodchandran: Space-efficient algorithms for reachability in surface-embedded graphs. In Proc. 27th IEEE Conf. on Comput. Complexity (CCC’12), pp. 326–333. IEEE Comp. Soc., 2012. [doi:10.1109/CCC.2012.15, ECCC:TR10-154]

[16]   Avi Wigderson: The complexity of graph connectivity. In Proc. Internat. Symp. Math. Foundations of Comp. Sci. (MFCS’92), pp. 112–132. Springer, 1992. [doi:10.1007/3-540-55808-X_10]