Robust Lower Bounds for Communication and Stream Computation
by Amit Chakrabarti, Graham Cormode, and Andrew McGregor
Theory of Computing, Volume 12(10), pp. 1-35, 2016
Bibliography with links to cited articles
[1] Farid M. Ablayev: Lower bounds for one-way probabilistic communication complexity and their application to space complexity. Theoret. Comput. Sci., 157(2):139–159, 1996. Preliminary version in ICALP’93. [doi:10.1016/0304-3975(95)00157-3]
[2] Alfred V. Aho, Jeffrey D. Ullman, and Mihalis Yannakakis: On notions of information transfer in VLSI circuits. In Proc. 15th STOC, pp. 133–139. ACM Press, 1983. [doi:10.1145/800061.808742]
[3] Noga Alon, Yossi Matias, and Mario Szegedy: The space complexity of approximating the frequency moments. J. Comput. System Sci., 58(1):137–147, 1999. Preliminary version in STOC’96. [doi:10.1006/jcss.1997.1545]
[4] Ziv Bar-Yossef, T. S. Jayram, Ravi Kumar, and D. Sivakumar: An information statistics approach to data stream and communication complexity. J. Comput. System Sci., 68(4):702–732, 2004. Preliminary version in FOCS’02. [doi:10.1016/j.jcss.2003.11.006]
[5] Ziv Bar-Yossef, T. S. Jayram, Ravi Kumar, D. Sivakumar, and Luca Trevisan: Counting distinct elements in a data stream. In Proc. 6th Internat. Workshop on Randomization and Computation (RANDOM’02), volume 2483 of LNCS, pp. 1–10. Springer, 2002. [doi:10.1007/3-540-45726-7_1]
[6] Amit Chakrabarti, Graham Cormode, and Andrew McGregor: Robust lower bounds for communication and stream computation. In Proc. 40th STOC, pp. 641–650. ACM Press, 2008. [doi:10.1145/1374376.1374470]
[7] Amit Chakrabarti, Graham Cormode, and Andrew McGregor: A near-optimal algorithm for computing the entropy of a stream. ACM Trans. Algorithms, 6:51:1–51:21, 2010. Preliminary version in SODA’07. [doi:10.1145/1798596.1798604]
[8] Amit Chakrabarti, T. S. Jayram, and Mihai Pătraşcu: Tight lower bounds for selection in randomly ordered streams. In Proc. 19th Ann. ACM-SIAM Symp. on Discrete Algorithms (SODA’08), pp. 720–729. ACM Press, 2008. ACM DL.
[9] Amit Chakrabarti, Subhash Khot, and Xiaodong Sun: Near-optimal lower bounds on the multi-party communication complexity of set disjointness. In Proc. 18th IEEE Conf. on Computational Complexity (CCC’03), pp. 107–117. IEEE Comp. Soc. Press, 2003. [doi:10.1109/CCC.2003.1214414]
[10] Amit Chakrabarti and Oded Regev: An optimal lower bound on the communication complexity of gap-hamming-distance. SIAM J. Comput., 41(5):1299–1317, 2012. Preliminary versions in STOC’11 and ECCC. [doi:10.1137/120861072, arXiv:1009.3460]
[11] Amit Chakrabarti, Yaoyun Shi, Anthony Wirth, and Andrew Chi-Chih Yao: Informational complexity and the direct sum problem for simultaneous message complexity. In Proc. 42nd FOCS, pp. 270–278. IEEE Comp. Soc. Press, 2004. [doi:10.1109/SFCS.2001.959901]
[12] Thomas M. Cover and Joy A. Thomas: Elements of Information Theory (2nd ed.). Wiley-Interscience, 2006.
[13] Erik D. Demaine, Alejandro López-Ortiz, and J. Ian Munro: Frequency estimation of internet packet streams with limited space. In Proc. 10th Ann. European Symp. on Algorithms (ESA’02), volume 2461 of LNCS, pp. 348–360. Springer, 2002. [doi:10.1007/3-540-45749-6_33]
[14] Jeff Edmonds and Russell Impagliazzo: Towards time-space lower bounds on branching programs. Unpublished manuscript, 1993. Available on author’s website.
[15] Joan Feigenbaum, Sampath Kannan, Andrew McGregor, Siddharth Suri, and Jian Zhang: Graph distances in the data-stream model. SIAM J. Comput., 38(5):1709–1727, 2008. Preliminary version in SODA’05. [doi:10.1137/070683155]
[16] Joan Feigenbaum, Sampath Kannan, Martin Strauss, and Mahesh Viswanathan: An approximate L1 difference algorithm for massive data streams. SIAM J. Comput., 32(1):131–151, 2002. Preliminary version in FOCS’99. [doi:10.1137/S0097539799361701]
[17] Philippe Flajolet and G. Nigel Martin: Probabilistic counting algorithms for data base applications. J. Comput. System Sci., 31(2):182–209, 1985. [doi:10.1016/0022-0000(85)90041-8]
[18] Sumit Ganguly: Counting distinct items over update streams. Theoret. Comput. Sci., 378(3):211–222, 2007. Preliminary version in ISAAC’05. [doi:10.1016/j.tcs.2007.02.031]
[19] Michael B. Greenwald and Sanjeev Khanna: Space-efficient online computation of quantile summaries. In ACM SIGMOD Internat. Conf. on Managment of Data, pp. 58–66. ACM Press, 2001. [doi:10.1145/375663.375670]
[20] Andre Gronemeier: Asymptotically optimal lower bounds on the NIH-multi-party information complexity of the AND-function and disjointness. In Proc. 26th Symp. Theoretical Aspects of Comp. Sci. (STACS’09), volume 3 of LIPIcs, pp. 505–516. Dagstuhl Publishing, 2009. [doi:10.4230/LIPIcs.STACS.2009.1846, arXiv:0902.1609]
[21] Sudipto Guha, Piotr Indyk, and Andrew McGregor: Sketching information divergences. Machine Learning, 72(1):5–19, 2008. [doi:10.1007/s10994-008-5054-x]
[22] Sudipto Guha and Andrew McGregor: Space-efficient sampling. In Proc. 11th Internat. Conf. on Artificial Intelligence and Stat. (AISTATS’07), volume 2 of JMLR Proceedings, pp. 171–178. JMLR, 2007. JMLR.org.
[23] Sudipto Guha and Andrew McGregor: Stream order and order statistics: Quantile estimation in random-order streams. SIAM J. Comput., 38(5):2044–2059, 2009. Preliminary version in ICALP’07. [doi:10.1137/07069328X]
[24] Sudipto Guha, Andrew McGregor, and Suresh Venkatasubramanian: Streaming and sublinear approximation of entropy and information distances. ACM Trans. Algorithms, 5(4):35:1–35:16, 2009. Preliminary version in SODA’06. [doi:10.1145/1597036.1597038, arXiv:cs/0508122]
[25] Nicholas J. A. Harvey, Jelani Nelson, and Krzysztof Onak: Sketching and streaming entropy via approximation theory. In Proc. 49th FOCS, pp. 489–498. IEEE Comp. Soc. Press, 2008. [doi:10.1109/FOCS.2008.76]
[26] Monika Rauch Henzinger, Prabhakar Raghavan, and Sridhar Rajagopalan: Computing on data streams. In James M. Abello and Jeffrey Scott Vitter, editors, External Memory Algorithms, volume 50 of DIMACS Ser. in Discr. Math. and Theoret. Comput. Sci., pp. 107–118. Amer. Math. Soc., 1999. ACM DL.
[27] Piotr Indyk and David P. Woodruff: Tight lower bounds for the distinct elements problem. In Proc. 44th FOCS, pp. 283–288. IEEE Comp. Soc. Press, 2003. [doi:10.1109/SFCS.2003.1238202]
[28] Piotr Indyk and David P. Woodruff: Optimal approximations of the frequency moments of data streams. In Proc. 37th STOC, pp. 202–208. ACM Press, 2005. [doi:10.1145/1060590.1060621]
[29] T. S. Jayram, Ravi Kumar, and D. Sivakumar: Two applications of information complexity. In Proc. 35th STOC, pp. 673–682. ACM Press, 2003. [doi:10.1145/780542.780640]
[30] T. S. Jayram, Ravi Kumar, and D. Sivakumar: The one-way communication complexity of Hamming distance. Theory of Computing, 4(6):129–135, 2008. [doi:10.4086/toc.2008.v004a006]
[31] Hartmut Klauck, Ashwin Nayak, Amnon Ta-Shma, and David Zuckerman: Interaction in quantum communication and the complexity of set disjointness. IEEE Trans. Inform. Theory, 53(6):1970–1982, 2007. Preliminary version in STOC’01. [doi:10.1109/TIT.2007.896888]
[32] Eyal Kushilevitz and Noam Nisan: Communication Complexity. Cambridge Univ. Press, 1997.
[33] Tak Wah Lam and Walter L. Ruzzo: Results on communication complexity classes. J. Comput. System Sci., 44(2):324–342, 1992. Preliminary version in SCT’89. [doi:10.1016/0022-0000(92)90025-E]
[34] Peter Bro Miltersen, Noam Nisan, Shmuel Safra, and Avi Wigderson: On data structures and asymmetric communication complexity. J. Comput. System Sci., 57(1):37–49, 1998. Preliminary version in STOC’95. [doi:10.1006/jcss.1998.1577]
[35] J. Ian Munro and Mike Paterson: Selection and sorting with limited storage. Theoret. Comput. Sci., 12(3):315–323, 1980. Preliminary version in FOCS’78. [doi:10.1016/0304-3975(80)90061-4]
[36] Christos H. Papadimitriou and Michael Sipser: Communication complexity. J. Comput. System Sci., 28(2):260–269, 1984. Preliminary version in STOC’82. [doi:10.1016/0022-0000(84)90069-2]
[37] Pavel Pudlák and Jiří Sgall: An upper bound for a communication
game related to time-space tradeoffs. In The Mathematics of Paul Erd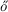 s I, pp. 399–407. Springer, 2013. Preliminary version (1995) in ECCC.
[doi:10.1007/978-1-4614-7258-2_24]
s I, pp. 399–407. Springer, 2013. Preliminary version (1995) in ECCC.
[doi:10.1007/978-1-4614-7258-2_24]
[38] Pranab Sen and Srinivasan Venkatesh: Lower bounds for predecessor searching in the cell probe model. J. Comput. System Sci., 74(3):364–385, 2008. Preliminary version in CCC’03. [doi:10.1016/j.jcss.2007.06.016, arXiv:cs/0309033]
[39] Alexander A. Sherstov: The communication complexity of gap Hamming distance. Theory of Computing, 8(8):197–208, 2012. Preliminary version in ECCC. [doi:10.4086/toc.2012.v008a008]
[40] Miklós Simonovits: Extremal graph theory. In Lowell W. Beineke and Robin J. Wilson, editors, Selected Topics in Graph Theory, volume 2, pp. 161–200. Academic Press, 1983.
[41] Thomas Vidick: A concentration inequality for the overlap of a vector on a large set, with application to the communication complexity of the gap-Hamming-distance problem. Chicago J. Theor. Comput. Sci., 2012(1), 2012. Preliminary version in ECCC. [doi:10.4086/cjtcs.2012.001]
[42] David P. Woodruff: Optimal space lower bounds for all frequency moments. In Proc. 15th Ann. ACM-SIAM Symp. on Discrete Algorithms (SODA’04), pp. 167–175. ACM Press, 2004. ACM DL.
[43] David P. Woodruff: The average-case complexity of counting distinct elements. In Proc. 13th Internat. Conf. on Database Theory (ICDT’09), volume 361 of ACM Internat. Conf. Proc. Series, pp. 284–295. ACM Press, 2009. [doi:10.1145/1514894.1514928]
[44] Andrew Chi-Chih Yao: Some complexity questions related to distributive computing (preliminary report). In Proc. 11th STOC, pp. 209–213. ACM Press, 1979. [doi:10.1145/800135.804414]
