New Lower Bounds for the Border Rank of Matrix Multiplication
by Joseph M. Landsberg and Giorgio Ottaviani
Theory of Computing, Volume 11(11), pp. 285-298, 2015
Bibliography with links to cited articles
[1] Sanjeev Arora and Boaz Barak: Computational Complexity: A Modern Approach. Cambridge Univ. Press, 2009.
[2] Markus Bläser: A 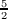 n2-lower bound for the rank of n × n-matrix
multiplication over arbitrary fields. In Proc. 40th FOCS, pp. 45–50. IEEE
Comp. Soc. Press, 1999. [doi:10.1109/SFFCS.1999.814576]
n2-lower bound for the rank of n × n-matrix
multiplication over arbitrary fields. In Proc. 40th FOCS, pp. 45–50. IEEE
Comp. Soc. Press, 1999. [doi:10.1109/SFFCS.1999.814576]
[3] Peter Bürgisser, Michael Clausen, and Mohammad Amin Shokrollahi: Algebraic Complexity Theory. Volume 315 of Grundlehren der mathematischen Wissenschaften. Springer, 1997. [doi:10.1007/978-3-662-03338-8]
[4] Peter Bürgisser and Christian Ikenmeyer: Geometric complexity theory and tensor rank. In Proc. 43rd STOC, pp. 509–518. ACM Press, 2011. [doi:10.1145/1993636.1993704, arXiv:1011.1350]
[5] Xi Chen, Neeraj Kayal, and Avi Wigderson: Partial derivatives in arithmetic complexity and beyond. Foundations and Trends in Theoretical Computer Science, 6(1-2):1–138, 2011. [doi:10.1561/0400000043]
[6] William Fulton and Joe Harris: Representation Theory. Volume 129 of Graduate Texts in Mathematics. Springer, 1991. [doi:10.1007/978-1-4612-0979-9]
[7] Ankit Gupta, Pritish Kamath, Neeraj Kayal, and Ramprasad Saptharishi: Approaching the chasm at depth four. J. ACM, 61(6):33:1–33:16, 2014. Preliminary versions in ECCC and CCC’13. [doi:10.1145/2629541]
[8] Jonathan D. Hauenstein, Christian Ikenmeyer, and Joseph M. Landsberg: Equations for lower bounds on border rank. Experimental Mathematics, 22(4):372–383, 2013. [doi:10.1080/10586458.2013.825892]
[9] Neeraj Kayal: An exponential lower bound for the sum of powers of bounded degree polynomials. Electron. Colloq. on Comput. Complexity (ECCC), TR12-081, 2012.
[10] Joseph M. Landsberg: The border rank of the multiplication of 2 × 2 matrices is seven. J. Amer. Math. Soc., 19(2):447–459, 2006. [doi:10.1090/S0894-0347-05-00506-0, arXiv:math/0407224]
[11] Joseph M. Landsberg: Tensors: Geometry and Applications. Volume 128 of Graduate Studies in Mathematics. Amer. Math. Soc., Providence, 2012. [doi:10.1090/gsm/128]
[12] Joseph M. Landsberg: New lower bounds for the rank of matrix multiplication. SIAM J. Comput., 43(1):144–149, 2014. [doi:10.1137/120880276, arXiv:1206.1530]
[13] Joseph M. Landsberg: Nontriviality of equations and explicit tensors in Cm ⊗ Cm ⊗ Cm of border rank at least 2m - 2. J. Pure Appl. Algebra, 219(8):3677–3684, 2015. [doi:10.1016/j.jpaa.2014.12.016]
[14] Joseph M. Landsberg and Giorgio Ottaviani: Equations for secant varieties of Veronese and other varieties. Annali di Matematica Pura ed Applicata, 192(4):569–606, 2013. [doi:10.1007/s10231-011-0238-6]
[15] François Le Gall: Powers of tensors and fast matrix multiplication. In Proceedings of the 39th Int. Symp. on Symb. and Alg. Comput. (ISSAC’14), pp. 296–303. ACM, New York, 2014. [doi:10.1145/2608628.2608664, arXiv:1401.7714]
[16] Thomas Lickteig: A note on border rank. Inf. Process. Lett., 18(3):173–178, 1984. [doi:10.1016/0020-0190(84)90023-1]
[17] Alex Massarenti and Emanuele Raviolo: The rank of n × n matrix
multiplication is at least 3n2 - 2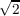 n
n - 3n. Linear Algebra Appl.,
438(11):4500–4509, 2013. [doi:10.1016/j.laa.2013.01.031]
- 3n. Linear Algebra Appl.,
438(11):4500–4509, 2013. [doi:10.1016/j.laa.2013.01.031]
[18] Alex Massarenti and Emanuele Raviolo: Corrigendum to “The rank of
n×n matrix multiplication is at least 3n2 - 2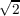 n
n - 3n”. Linear Algebra
Appl., 445:369–371, 2014. [doi:10.1016/j.laa.2013.12.009]
- 3n”. Linear Algebra
Appl., 445:369–371, 2014. [doi:10.1016/j.laa.2013.12.009]
[19] Ketan D. Mulmuley and Milind A. Sohoni: Geometric complexity theory I: an approach to the P vs. NP and related problems. SIAM J. Comput., 31(2):496–526, 2001. [doi:10.1137/S009753970038715X]
[20] Giorgio Ottaviani: Symplectic bundles on the plane, secant varieties and Lüroth quartics revisited. In Vector bundles and low codimensional subvarieties: state of the art and recent developments, volume 21 of Quad. Mat., pp. 315–352. Dept. Math., Seconda Univ. Napoli, Caserta, 2007. [arXiv:math/0702151]
[21] Claudio Procesi: Lie Groups: An Approach through Invariants and Representations. Universitext. Springer, 2007. [doi:10.1007/978-0-387-28929-8]
[22] Alexey V. Smirnov: The bilinear complexity and practical algorithms for matrix multiplication. Comput. Math. Math. Phys., 53(12):1781–1795, 2013. [doi:10.1134/S0965542513120129]
[23] Volker Strassen: Gaussian elimination is not optimal. Numer. Math., 13(4):354–356, 1969. [doi:10.1007/BF02165411]
[24] Volker Strassen: Rank and optimal computation of generic tensors. Linear Algebra Appl., 52-53:645–685, 1983. [doi:10.1016/0024-3795(83)80041-X]
[25] Avi Wigderson: P, NP and mathematics—a computational complexity perspective. In International Congress of Mathematicians. Vol. I, pp. 665–712. Eur. Math. Soc., Zürich, 2007. [doi:10.4171/022-1/25]
